Abstract
The prestressed UHPC-RC I-shaped composite beam is a common new type of beam structure at present, and there is relatively little research on the torsional calculation method for this type of structure. This article first defines the mechanical concept of characteristic torque based on the structural characteristics and different stage stress states of prestressed UHPC-RC I-shaped composite beams. Considering the initial pre stress, UHPC tensile strength, and concrete tensile and compressive stress states, theoretical formulas for initial cracking torque, cracking torque, and ultimate torque are derived based on elastic theory, plastic theory, and variable angle spatial truss theory, respectively; Subsequently, taking a 25m prestressed UHPC-RC I-shaped composite beam as an example, the accuracy of the theoretical formula in this paper was verified through finite element calculation results, where the theoretical value of the ultimate torque differed only 2.3% from the finite element calculation value. Finally, a parametric analysis of the characteristic torque of the beam was conducted, and the results of this study showed that the initial cracking torque value of the section was not affected by the initial pre stress and UHPC tensile strength, provided that the main tensile stress of the bottom concrete did not exceed the limit; Increasing the initial prestressing stress of the section or enhancing the tensile strength of UHPC can enhance the cracking torque and ultimate torque of the section. Considering the initial prestressing stress and UHPC tensile strength, the ultimate torque of the section can be increased by 57.9% and 94.1%, respectively. If the influence of the tensile and compressive stress states of concrete is neglected in the calculation, the values of the initial cracking torque and cracking torque of the section will be overestimated by 8.6% and 13.3%, respectively.
|
Published in
|
American Journal of Civil Engineering (Volume 13, Issue 4)
|
|
DOI
|
10.11648/j.ajce.20251304.14
|
|
Page(s)
|
222-234 |
|
Creative Commons
|

This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
|
|
Copyright
|
Copyright © The Author(s), 2025. Published by Science Publishing Group
|
Keywords
Prestressed UHPC-RC Composite Beam, I-Shaped Cross-section, Characteristic Torque, Theoretical Analysis, Method of Calculation
1. Introduction
Prestressed UHPC-RC I-shaped composite beam is a new type of beam structure, which has the advantages of high structural strength, light weight, high material utilization rate, small lifting weight on site, convenient maintenance in the later stage and so on
. At present, there are more studies on the bending and shear mechanical properties of this kind of structure, but less on the torsional properties. However, the torsion resistance of I-section is poor, which may produce large section torque due to the bending torsion coupling effect or eccentric load effect of curved beam in practical engineering. It is necessary to accurately analyze the torsion resistance of section in the design stage.
At present, the design codes (standards) for concrete (UHPC) structures at home and abroad are mainly the calculation formulas of cracking torque and ultimate torque for rectangular or box section. The domestic
| [3] | JTG 3362-2018, Design Specification for Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. China Communications Press, 2018. |
[3]
and European
| [4] | EN 1992-2: 2005. Eurocode 2: Design of Concrete Structures-Concrete Bridges Design and Detailing Rules [S]. 2008. |
| [5] | NF P 18-710. National addition to Eurocode 2 - Design of concrete structures: specific rules for Ultra-High Performance Fibre-Reinforced Concrete (UHPFRC) [S]. Association Française de Normalisation, 2016. |
[4, 5]
concrete structure design codes put forward the contribution of prestress effect to the ultimate torque. The French
| [6] | ULTRA HIGH PERFORMANCE FIBRE- REINFORCED (Recommendation, Revised edition) [S]. Association Française de Génie Civil, 2013. |
[6]
and Swiss
| [7] | Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC) - Construction material, dimensioning and application (Recommendation) [S]. MCS-EPFL Lausanne, Switzerland, 2016. |
[7]
UHPC design codes include the contribution of UHPC tensile strength to the ultimate torque. The torsional calculation formula in the domestic UHPC design code
| [8] | T/CBMF 185-2022, Specifcation for design of ultra-high performance concrete struetures [S]. China Building Materials Industry Press, 2022. |
| [9] | T/CECS G: D60-02-2023, Technical Specifications for Highway Ultra-high Performance Concrete (UHPC) Bridges [S]. People's Communications Publishing House Co., Ltd, 2023. |
| [10] | JGJ/T 465-2019, Standard for design of steel fiber reinforced concrete structures [S]. China Architecture&Building Press, 2019. |
[8-10]
is the same as that in the pre specification
| [3] | JTG 3362-2018, Design Specification for Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. China Communications Press, 2018. |
[3]
. The existing code formulas are not suitable for calculating the characteristic torque of prestressed UHPC-RC I-beams. In recent years, scholars at home and abroad have made some achievements in the research of UHPC beam characteristic torque calculation method
| [11] | ZHOU J, Li C, Experimental investigation on torsional behaviors of ultra-high performance fiber reinforced concrete hollow beams [J]. Cement and Concrete Composites, 2022. CECO: 104504. https://doi.org/10.1016/j.cemconcomp.2022.104504 |
| [12] | KWAHK I, JOHC, LEE JW, Torsional behavior design of UHPC box beams based on thin-walled tube theory [J]. Engineering, 2015, 7(3): 101-114. https://doi.org/10.4236/eng.2015.73009 |
| [13] | YANG I, JOH C, LEE JW, et al. Torsional behavior of ultra high performance concrete squared beams [J]. Engineering Structures, 2013(56): 372-383. https://doi.org/10.1016/j.engstruct.2013.05.027 |
| [14] | Qiu JS. Study on calculation theory and behavior of steel fiber reinforced concrete Multi-ribbed composite slab [D]. Xi'an University of Architecture and Technology, 2011. |
| [15] | Ke L, Yu S, Li CX, etc. Torsional Performance and Bearing Capacity Calculation of Reinforced UHPC Rectangular Beams Subjected to Combined Bending-shear-torsion [J]. China Journal of Highway and Transport, 2023, 36(09): 157-171. https://doi.org/10.19721/j.cnki.1001-7372.2023.09.013 |
| [16] | Wang JQ, Zhou C, Jia WB, etc. Investigation on the Effect of Steel Fiber Property on the Torsional Performance of Ultra high Performance Concrete Rectangular Beams without Steel Reinforcement [J]. China Journal of Highway and Transport, 2022, 35(12): 115-129. https://doi.org/10.19721/j.cnki.1001-7372.2022.12.010 |
[11-16]
. According to the research of some scholars
| [11] | ZHOU J, Li C, Experimental investigation on torsional behaviors of ultra-high performance fiber reinforced concrete hollow beams [J]. Cement and Concrete Composites, 2022. CECO: 104504. https://doi.org/10.1016/j.cemconcomp.2022.104504 |
| [12] | KWAHK I, JOHC, LEE JW, Torsional behavior design of UHPC box beams based on thin-walled tube theory [J]. Engineering, 2015, 7(3): 101-114. https://doi.org/10.4236/eng.2015.73009 |
| [13] | YANG I, JOH C, LEE JW, et al. Torsional behavior of ultra high performance concrete squared beams [J]. Engineering Structures, 2013(56): 372-383. https://doi.org/10.1016/j.engstruct.2013.05.027 |
[11-13]
, the torsional bearing capacity of reinforced UHPC beams is mainly determined by the amount and type of steel fiber, reinforcement ratio and section form. Steel fiber can significantly improve the section cracking torque and ultimate torque. Wang JQ et al.
| [16] | Wang JQ, Zhou C, Jia WB, etc. Investigation on the Effect of Steel Fiber Property on the Torsional Performance of Ultra high Performance Concrete Rectangular Beams without Steel Reinforcement [J]. China Journal of Highway and Transport, 2022, 35(12): 115-129. https://doi.org/10.19721/j.cnki.1001-7372.2022.12.010 |
[16]
carried out the pure torsion performance test of unreinforced UHPC rectangular beam, and proposed the calculation formula of cracking and ultimate torque of unreinforced UHPC rectangular beam based on the test data. Zhou C et al.
took the RC beam strengthened by UHPC thin layer as the research object, deduced the calculation formula of torsional bearing capacity of hooped UHPC hollow rectangular beam, and verified it by model test. Li CX et al.
proposed the cracking torque coefficient of UHPC members and the section torsional coefficient in the ultimate torque formula through pure torsion model test. Li CX et al.
| [19] | Li CX, Yu S, Zhou LD, etc. Torsional performance of UHPC beams with flanges and unified formula for characteristic torques [J]. Journal of Civil Engineering, 2023, 56(12): 82-97. https://doi.org/10.15951/j.tmgcxb.22080863 |
[19]
carried out the pure torsion test of two reinforced UHPC box girders with flanges, collected the test data of 47 groups of UHPC specimens, and proposed the calculation formula of ultimate torque suitable for rectangular and box section beams.
To sum up, the current research object is mainly focused on the reinforced UHPC rectangular beam, a small number of literatures involve the reinforced UHPC box beam, but not the prestressed UHPC-RC I-shaped composite beam. The existing research failed to put forward the calculation formula of initial crack torque reflecting the elastic torsional limit state. The existing characteristic torque calculation formula is mainly based on the fitting formula proposed by the model test data, and most of them can not take into account the effect of prestress, the reduction effect of tensile strength of concrete under tension and compression stress state, and the influence of UHPC post crack strength. Therefore, it is necessary to study the torsional calculation method of prestressed UHPC-RC I-shaped composite beam according to its mechanical characteristics. In this chapter, according to the mechanical characteristics of UHPC-RC I-beam under normal use and ultimate bearing capacity, the mechanical concept of section characteristic torque is proposed, and the theoretical formulas of section initial cracking torque, cracking torque and ultimate torque are derived. The theoretical formulas are verified by finite element calculation results, and finally the variable parameter analysis of engineering examples is carried out.
2. Theoretical Analysis of Characteristic Torque
2.1. Concept of Characteristic Torque Mechanics
The characteristic torque of UHPC-RC I-shaped composite beam reflects the process of the beam body from elastic torsion state to ultimate breaking cycle state: the initial cracking torque refers to the external torque corresponding to the moment when the principal tensile stress at any point on the section reaches the tensile strength of concrete; Cracking torque refers to the external torque when the full section reaches the yield strength of concrete and the section enters the full plastic state; Ultimate torque refers to the external torque corresponding to the section reaching the ultimate failure state. In the following, the torsional section zoning method of I-shaped composite beams is proposed, and then the theoretical formula of characteristic torque is derived according to the corresponding mechanical concepts.
2.2. Torsional Section Zoning and Section Stress Calculation Method
According to the distribution characteristics of shear flow in the section of I-beam under torsion, the section of standard I-beam composite beam is divided into ABC three block areas. Block B and block C correspond to UHPC beam, and block A corresponds to RC bridge deck. For prestressed UHPC beams, the width of the web is usually less than the thickness of the bridge deck and bottom plate. According to the principle of the maximum sum of torsional stiffness of each block area after section division, the section division is carried out in the way that the web block area does not extend to the bridge deck and bottom plate, as shown in
Figure 1. It should be noted that when the roof area of UHPC beam is large, a UHPC beam roof block area should be added in
Figure 1 (similar to the section in
Figure 3).
Figure 1. Anti torsion section zoning diagram.
The prestressed UHPC-RC composite beam shall be prefabricated with UHPC beam (block B+block C), and then the RC bridge deck (block A) shall be poured and the secondary load shall be applied. The section stress of each block area shall be calculated according to the specific construction process.
The section stress (positive under pressure) of block A, block B and block C is:
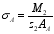 (1)
(1) 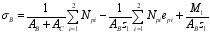 (2)
(2) 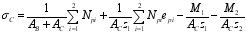 (3)
(3) Where: Npi is the resultant force of part i steel tendon; epi is the distance between the i-part tendon and the gravity center axis of the section; z1 is the distance between the upper and lower centroids of the center of gravity axis of UHPC section (block B+block C) when the beam is subjected to bending moment. When the area of UHPC top plate and bottom plate is larger than that of the web, the distance between the top and bottom plate tendon positions can be taken; When the area of UHPC top plate or bottom plate is slightly larger or smaller than that of the web, 2/3 of the overall section height can be taken; z2 is the distance between the upper and lower centroids of the gravity axis of the overall section (block A+block B+block C) when the beam is subjected to bending moment. When the area of the bridge deck or bottom slab is much larger than that of the web, the distance between the bottom slab tendon and the center of gravity axis of the bridge deck can be taken; AA, AB and AC are the sectional areas of blocks A, B and C; M1 is the section bending moment caused by the dead weight of RC bridge deck and UHPC beam; M2 is the section bending moment caused by phase II load.
2.3. Initial Cracking Torque
The initial cracking torque is analyzed according to the elastic theory, and the theoretical formula of the initial cracking torque of I-section is derived below. When the concrete is in tension and compression stress state, the tensile strength of concrete decreases. According to the specification
| [20] | GB 50010-2010, Code for design of concrete structures [S]. China Communications Press, 2015. |
[20]
, the following formula is given:
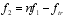 (4)
(4) 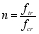 (5)
(5) Where: f1 and f2 are the compressive strength (positive value) and tensile strength (negative value) under biaxial tensile and compressive stress state; ftr and fcr are the compressive strength (positive value) and tensile strength (positive value) under uniaxial stress state.
The maximum principal tensile and compressive stresses of the section in block i are:
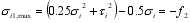 (6)
(6) 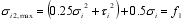 (7)
(7) Where: σi, τi are the normal stress and shear stress of the section in the block area i; σi is positive under pressure.
The following equation can be derived from simultaneous equation (
4), equation (
6) and equation (
7):
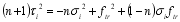 (8)
(8) Then the maximum shear stress of the section in block i is:
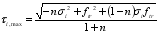 (9)
(9) According to the elastic torsion theory, the section torsion rate of each block area is the same, and each block area shares the torque according to the proportion of its torsional stiffness in the total section stiffness, so the overall section torque corresponding to the maximum shear stress of each block area section is:
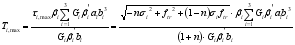 (10)
(10) Where: Gi is the shear modulus corresponding to the block area i; βi, βi' is the torsion factor; ai and bi are the lengths of the long and short sides of the section.
When
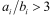
,
, there are:
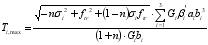 (11)
(11) The initial cracking torque of the overall section is the minimum value of the overall section torque corresponding to the section of each block:
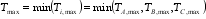 (12)
(12) 2.4. Cracking Torque
The section cracking torque is analyzed according to the plastic theory, and the theoretical formula of I-section cracking torque is derived below. When the block I reaches the full section plastic state, the full section shear stress should reach the limit value. Considering the influence of concrete tension and compression stress state on tensile strength, the maximum shear stress of section I in block area can be expressed as formula (
9), and the section cracking torque of block area I can be expressed as:
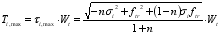 (13)
(13) Where: Wt is the torsional plastic resistance moment of the section.
When the section of block
i is rectangular, equation (
13) can be written as:
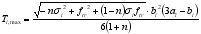 (14)
(14) The cracking torque of the overall section is the sum of the cracking torques of the sections in each block:
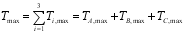 (15)
(15) 2.5. Ultimate Torque
The ultimate torque is analyzed according to the theory of variable angle space truss model, and the theoretical formula of the ultimate torque of I-section is derived below.
2.5.1. Basic Assumptions
Figure 2. Variable angle spatial truss model.
The variable angle space truss model is a classical mechanical model for analyzing the torsional limit state of components, as shown in
Figure 2. The basic assumptions of the variable angle space truss model are as follows:
(1) The inclined angle of the inclined compression bar of the truss composed of the concrete shell with spiral cracks is unified as α. The ordinary concrete inclined compression bar can only bear the compressive stress on the normal section, while the UHPC inclined compression bar can bear the compressive stress on the normal section and the tensile stress between the inclined compression bars at the same time;
(2) The longitudinal bars and stirrups only bear tensile force, and form the chord and web members of the truss respectively;
(3) The torsion resistance of core concrete and the pin bolt effect of reinforcement are ignored.
2.5.2. Ultimate Torque of Uhpc Beam (Block Areas B and C)
The ultimate torque analysis of UHPC beams (block areas B and C) should consider the post crack strength of UHPC between the gaps of the diagonal struts. The lower half of the space truss model (in the blue box of
Figure 2) is taken as the isolation body, which can be obtained from the vertical force balance relationship:
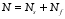 (16)
(16) Including:
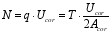 (17)
(17) 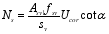 (18)
(18) 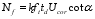 (19)
(19) Where:
q is the shear flow acting on the side wall;
ft is the post crack strength of UHPC;
fsv is the tensile strength of stirrup;
sv is the stirrup spacing;
Ns is the vertical tension provided by the single leg stirrup;
Nf is the vertical tension provided between the gaps of UHPC diagonal struts;
N is the vertical force formed by the cross-section shear flow (the sum of the vertical tension provided by the single leg stirrup and UHPC);
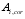
is the core area of section I in the blocking area,
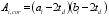
;
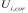
is the perimeter of the core area of section
i in the blocking area,
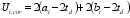
;
k is the fiber orientation coefficient; TD is the wall thickness of the equivalent thin-wall section,
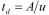
,
A is the total area surrounded by the outer periphery of the solid section;
u is the outer perimeter of the solid section. The equivalent wall thickness
td shall not be less than 2 times of the distance between the outer edge of the section and the center of the longitudinal reinforcement. For hollow sections, the actual wall thickness is the upper limit
| [4] | EN 1992-2: 2005. Eurocode 2: Design of Concrete Structures-Concrete Bridges Design and Detailing Rules [S]. 2008. |
[4]
.
Substituting equations (
17) to (
19) into equation (
16), we can get:
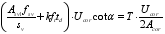 (20)
(20) Taking the overall space truss model as the isolation body, the horizontal balance relationship can be obtained:
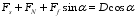 (21)
(21) According to the vertical balance relationship:
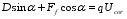 (22)
(22) Including:
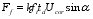 (23)
(23) 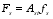 (24)
(24) 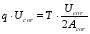 (25)
(25) Where: Fs is the sum of tensile force of longitudinal ordinary reinforcement; Ff is the tension force provided between the gaps of UHPC diagonal struts; FN is the section preloading stress generated by the prestressing beam; D is the sum of axial pressure of UHPC inclined compression rod; Ast is the sum of the areas of longitudinal ordinary reinforcement; fs is the tensile strength of longitudinal ordinary reinforcement.
Substituting equations (
23) to (
25) into equations (
21) to (
22), we can get:
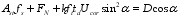 (26)
(26) 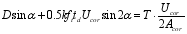 (27)
(27) The following formulas can be obtained from the mechanical equilibrium relationship of the above variable angle space truss model.
When stirrups yield:
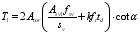 (28)
(28) When the longitudinal bars yield:
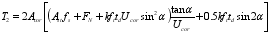 (29)
(29) When the stirrup and longitudinal reinforcement yield at the same time, the inclination angle α can be obtained according to
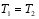
:
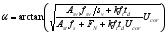 (30)
(30) 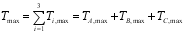 (31)
(31) 2.5.3. Ultimate Torque of Rc Bridge Deck (Block A)
The ultimate torque of block a is still considered according to the space truss theory, but the concrete will fail after cracking. It is sufficient to make FT in equations (
28) to (
30) zero.
3. Numerical Verification of Torsional Calculation
3.1. Example Parameters
This example is a prestressed pretensioned UHPC-RC I-shaped composite beam with a span of 25m
. The calculated span is 24m, and the beam section size is shown in
Figure 3. 5 and 36 steel strands are respectively arranged at the top and bottom plate, and the tension control stress under the anchor is 1395mpa. There is no ordinary reinforcement in the UHPC beam. Two layers of ordinary reinforcement mesh are arranged in the RC bridge deck with a reinforcement spacing of 100mm. The RC bridge deck is made of C50 concrete, the I-beam is made of UC150 grade UHPC, the ordinary reinforcement is HRB400 reinforcement, and the prestressed reinforcement is Φ
s15.2mm Prestressed steel strand. The material mechanical properties are shown in
Table 1.
Table 1. Material Mechanical Properties Table.
Material | Compressive strength (MPa) | Tensile strength (MPa) | Elastic modulus (MPa) | Poisson's ratio | Bulk density (kN/m3) |
C50 | 32.4 | 2.65 | 34500 | 0.2 | 26.0 |
UC150 | 105 | 7.2 | 43500 | 0.2 | 27.0 |
HRB400 | 400 | 400 | 200000 | 0.3 | 78.5 |
Prestressed steel strand | / | 1860 | 195000 | 0.3 | 78.5 |
Based on the sectional characteristics of the UHPC-RC I-beam, block area D belongs to post-cast construction and is mainly connected to block area A through shear reinforcement. At the same time, from a perspective of safety and for ease of calculation and analysis in practical projects, the beam section is divided into four block areas, as shown in
Figure 4. Block A, B and C correspond to the top plate, web plate and bottom plate of UHPC beam, and block D corresponds to RC bridge deck.
Figure 3. Sectional View of Example Beam.
Figure 4. Anti torsion section zoning diagram.
3.2. Establishment of Finite Element Model
The finite element model of the UHPC-RC I-shaped composite beam is established in the finite element analysis software Midas-FEA. The whole bridge is divided into 255909 elements and 296567 nodes. C50 concrete bridge deck is divided into 92000 units and 117735 nodes, and UHPC I-beam is divided into 119000 units and 146292 nodes. The bridge deck and I-beam grids are mainly divided into 50
3 mm
3 hexahedral elements, and some section transition sections are tetrahedral elements, as shown in
Figure 5. In order to simulate that the shear flow does not flow between the bridge deck and the I-beam top plate, an interface unit is set between the bottom surface of the bridge deck and the top surface of the I-beam. The interface can slip laterally without lifting.
Figure 5. Overall diagram of finite element model.
The finite element model simulates the fabrication and loading process of UHPC-RC I-shaped composite beam: firstly, precast the UHPC I-shaped beam and tension the pretensioned steel strand, pour the RC bridge deck, apply the secondary load, and finally apply the concentrated torque at the right end for loading. A rigid connection is set between the boundary point and the loading section at both ends. The constraint conditions of the left boundary point are TX, Ty, TZ, RX and RZ, and the constraint conditions of the right boundary point are Ty, TZ and RZ. The torsional load is applied to the right boundary point. The tensile properties of UHPC in the model are simulated using a simplified elasto-plastic constitutive model. The elastic modulus of UHPC remains constant until it reaches the elastic limit strain, and the tensile stress of UHPC within the range from the elastic limit strain to the ultimate tensile strain (0.0025) decreases linearly to zero. The tensile properties of C50 concrete are not neglected in the model and are also simulated using a simplified elasto-plastic constitutive model.
3.3. Finite Element Calculation Results
The load rotation curve of the example beam calculated by the finite element model is shown in
Figure 6. The development process of the plastic state of the example beam under torsion is shown in
Figure 7 through numerical simulation. It can be seen from the figure that the theoretical value of the initial cracking torque of the example beam is 133kN·m, the theoretical value of the cracking torque is 420kN·m, and the theoretical value of the ultimate torque is 741kN·m.
Figure 6. Numerical calculation results of beam load angle curve for example.
Figure 7. Development process of plastic state of example beam under torsional action.
3.4. Numerical Verification of Characteristic Torque
The calculation results based on the theoretical formula of characteristic torque deduced in this paper are shown in
Table 2. The theoretical value of ultimate torque is provided in two values depending on whether the tensile strength of C50 concrete is considered or not. 741.7 is the theoretical value without considering the tensile strength of C50, while 890.4 is the theoretical value with the tensile strength of C50 considered.
Table 2. Theoretical and Finite Element Calculation Values of Sectional Characteristic Torque.
Characteristic torque | Initial cracking torque | Cracking torque | Ultimate torque |
Theoretical value (C50 tensile strength is ignored for ultimate torque) | 133.1 | 420.5 | 741.7 |
Theoretical value (C50 tensile strength is considered for ultimate torque) | 133.1 | 420.5 | 890.4 |
Finite element calculation value | 144 | 480 | 912 |
It can be seen that the theoretical values of the initial cracking torque and the cracking torque of the beam section of the example are close to those calculated by the finite element method; When the tensile strength of bridge deck C50 concrete is considered, the theoretical values of the initial cracking torque, cracking torque and ultimate torque of the example beam section are close to those calculated by the finite element method. It shows that the theoretical formula of characteristic torque of prestressed UHPC-RC I-shaped composite beam proposed in this paper can truly reflect the torsional process of the example beam. For the sake of safety, this paper suggests that the contribution of concrete tensile strength should not be considered in the calculation of bridge deck ultimate torque, and the subsequent analysis should also ignore the tensile strength of C50 concrete.
4. Characteristic Torque Parameter Analysis
According to the example parameters in Section 2.1, based on the theoretical formula of characteristic torque, the variable parameter analysis of preloading stress, UHPC tensile (post crack) strength and concrete tensile and compressive stress state is carried out to study the influence of the parameters on the torsional performance of prestressed UHPC-RC I-shaped composite beams.
4.1. Initial Preloading Stress
4.1.1. Effect on Initial Cracking Torque
The effect of initial preloading stress on initial cracking torque value is shown in
Figure 8. The preloading stress values are taken as 125%, 100%, 75%, 50%, 25% and 0% of the original value of the example beam (without prestress). When the preloading stress value is greater than 25% of the original value (100%), the overall section initial cracking torque is 133.1kN·m, and when it is less than 25% of the original value, the overall section initial cracking torque is 0.
The initial cracking torque TICA of block a increases with the decrease of preloading stress, but the increase of initial cracking torque is also small due to the small increase of section normal stress. The initial cracking torques ticb and TICC of block B and C decrease with the decrease of preloading stress. Because the normal stress of the section decreases greatly, the initial cracking torque also decreases greatly. When the preloading stress value is reduced to 25% of the original value, although the sectional tensile stress of 2.6MPa is generated in the block C, the maximum principal tensile stress of the section does not exceed the tensile strength of UHPC, and the block C can still withstand a certain torque. When the preloading stress value drops to 0%, the sectional tensile stress of 10.06mpa is generated in the block C, and the section has cracked, and its initial cracking torque is 0. Block D (RC bridge deck) is a post pouring construction. The normal stress of the section is not affected by the preloading stress, and its cracking torque remains unchanged.
Figure 8. Initial preloading stress initial cracking torque.
4.1.2. Effect on Cracking Torque
The effect of initial preloading stress on the cracking torque value is shown in
Figure 9. The cracking torque of the overall section is 439.5kN·m, 420.5kN·m, 393.9kN·m, 356.4kN·m, 297.5kN·m, 195.1kN·m.
The cracking torques TCRA, TCRB and TCRD of block a, B and D are less affected by the preloading stress value. The cracking torque tcrc of Block C decreases with the decrease of preloading stress. Due to the large reduction of normal stress of the section, the cracking torque also decreases greatly. The normal stress of the section in Block D is not affected by the preloading stress, and its cracking torque remains unchanged. The effect of initial preloading stress on cracking torque is the same as that of initial cracking torque. When the preloading stress value is reduced to 25% of the original value, although the sectional tensile stress is generated in the block C, its section does not enter the fully plastic state, and the block C can continue to bear the torque until the full section enters the plastic state. When the preloading stress value is reduced to 0%, the cracking torque of the whole section is reduced to 195.1kN·m, indicating that the preloading stress value has a great influence on the cracking torque of the whole section, and the preloading stress of the section should be appropriately increased.
Figure 9. Initial pre stress cracking torque.
4.1.3. Effect on Ultimate Torque
The effect of initial preloading stress on cracking angle and ultimate torque value is shown in
Figure 10 and
Figure 11, and the ultimate torque of the overall section is 779.7kN·m, 741.7kN·m, 697.7kN·m, 644.1kN·m, 566.7kN·m, 469.6kN·m.
The cracking angle θ a of block a decreases slightly with the decrease of preloading stress, while the cracking angles θ B and θ C of block B and C increase with the decrease of preloading stress. When the preloading stress value decreases to 0%, the normal stress of the section in Block B is 0, and the cracking angle θ B is 45°; The cracking angle θ C of Block C is about 90°, indicating that the tensile stress of the section of Block C has exceeded the strength of UHPC after cracking, and it can not continue to bear the torque. The cracking angle θ D of block D is not affected by the preloading stress. The effect of initial preloading stress on ultimate torque is the same as that of initial cracking torque and cracking torque. For Block C, the strut force in the space truss model is borne by the post crack stress of the crack gap between the struts. When the preloading stress value is reduced to 25% of the original value, the sectional tensile stress is generated in the block C, but the crack gap between the compression rods can still provide tensile capacity, and the block C still does not reach the limit torque. When the preloading stress value decreases to 0%, the tensile stress of section C in the block area has exceeded the limit, and the space truss model cannot be formed to resist the external torque. The calculation results show that increasing the preloading stress can improve the ultimate torque of the whole section.
Figure 10. Initial pre stress limit torque.
Figure 11. Initial pre stress cracking angle.
4.2. Effect of Uhpc Tensile Strength
4.2.1. Effect on Initial Cracking Torque
The effect of UHPC tensile strength on initial cracking torque value is shown in
Figure 12. The UHPC tensile strength values are taken as 125%, 100%, 75%, 50%, 25% and 0% of the example beam respectively (the section has no tensile capacity). When the UHPC tensile strength is greater than 25% of the original value (100%), the overall section initial crack torque is 133.1kN·m, and when it is less than 25% of the original value, the overall section initial crack torque decreases with the decrease of UHPC tensile strength.
The initial cracking torques TICA, ticb and TICC of block a, B and C gradually decreased with the decrease of UHPC tensile strength. When the tensile strength of UHPC is less than 25% of the original value, the initial cracking torque value of the overall section is controlled from block D to block C.
Figure 12. UHPC tensile strength initial cracking torque.
4.2.2. Effect on Cracking Torque
The effect of UHPC tensile strength on the cracking torque value is shown in
Figure 13. The cracking torque of the overall section is 462.7kN·m, 420.5kN·m, 374.3kN·m, 326.8kN·m, 261.0kN·m, 116.3kN·m.
Figure 13. UHPC tensile strength cracking torque.
The cracking torques TCRA, TCRB and tcrc of block a, B and C gradually decrease with the decrease of UHPC tensile strength. When the tensile strength of UHPC decreases to 0%, the plastic sections of block a, B and C cannot be formed. The tensile strength of UHPC has a great influence on the cracking torque value of the whole section, and appropriately increasing the tensile strength of the material can improve the cracking torque of the whole section.
4.2.3. Effect on Ultimate Torque
The effect of UHPC tensile strength on cracking angle and ultimate torque value is shown in
Figure 14 and
Figure 15, and the ultimate torque of the overall section is 796.7kN·m, 741.7kN·m, 683.4kN·m, 625.1kN·m, 547.3kN·m, 382.1kN·m.
The cracking angles θ a, θ B and θ C of block a, B and C decrease with the decrease of UHPC tensile strength. When the tensile strength of UHPC decreases to 0%, the cracking angle of block a, B and C is 0°, indicating that the space truss model cannot be formed in the block. The ultimate torques TUA, tub and TUC of block areas a, B and C decrease with the decrease of UHPC tensile strength. There is no reinforcement in block areas a, B and C, and the compressive bar force in the space truss model is borne by the post crack stress of the crack gap between the compressive bars. When the material matrix has no tensile capacity, the space truss model cannot be formed to resist the external torque. When the tensile strength of UHPC is reduced from the original value to 0%, the ultimate torque of the overall section can only be provided by block D. The post crack strength of UHPC has a great influence on the ultimate torque value of the overall section, so the post crack tensile strength of the material should be appropriately increased.
Figure 14. UHPC tensile strength ultimate torque.
Figure 15. UHPC tensile strength cracking angle.
4.3. Influence of Concrete Tension and Compression Stress State
When the concrete is in the tension and compression stress state, the tensile strength of the concrete decreases, which has a certain impact on the initial cracking torque and cracking torque value of the overall section. The calculation results of whether to consider the influence of the tension and compression stress state of the concrete are shown in
Table 3 and
Table 4. The initial cracking torque and cracking torque of the whole section were reduced by 8.6% and 13.3%, respectively. If the effect of concrete tension and compression stress state on tensile strength is ignored in the calculation, the initial cracking torque and cracking torque of the whole section will be overestimated.
Table 3. Concrete tensile and compressive stress state - initial cracking torque.
Whether to consider the tension and compression stress state of concrete | Torque value of section initial crack(kN·m) |
YES | Initial cracking torque in block area | TicA | TicB | TicC | TicD |
867.3 | 839.0 | 384.3 | 133.1 |
Initial cracking torque of overall section | Tic |
133.1 |
NO | Initial cracking torque in block area | TicA | TicB | TicC | TicD |
987.4 | 985.9 | 455.7 | 145.6 |
Initial cracking torque of overall section | Tic |
145.6 |
Table 4. Concrete tensile and compressive stress state cracking torque.
Whether to consider the tension and compression stress state of concrete | Section cracking torque value(kN·m) |
YES | Cracking torque in block area | TcrA | TcrB | TcrC | TcrD |
47.4 | 52.1 | 204.7 | 116.3 |
Overall section cracking torque | Tcr |
420.5 |
NO | Cracking torque in block area | TcrA | TcrB | TcrC | TcrD |
54.0 | 61.2 | 242.7 | 127.2 |
Overall section cracking torque | Tcr |
485.2 |
5. Conclusion
This article systematically studies the calculation method of characteristic torque for prestressed UHPC-RC I-shaped composite beams through theoretical analysis and numerical simulation. The main conclusions drawn are as follows:
(1) This article addresses the deficiencies of existing research by proposing a characteristic torque calculation formula based on the structural characteristics of prestressed UHPC-RC I-shaped composite beams. This formula takes into account the effects of prestressing, the tensile and compressive stress states of concrete, and the tensile strength of UHPC, providing a more accurate representation of the structure's torsion state compared to traditional formulas. The theoretical values of the initial cracking torque and cracking torque of the example beam differ by 7.6% and 12.6% from the finite element calculation values, respectively, while the ultimate torque (considering the tensile strength of C50) differs by only 2.3%, verifying the accuracy of the torsion calculation formula derived in this article. The torsion calculation formula in this article can accurately predict the torsion resistance of prestressed UHPC-RC I-shaped composite beams and can be applied to engineering design and safety assessment.
(2) Comparing the theoretical analysis and numerical calculation results of the characteristic torque of a 25m span beam, the theoretical values of the initial cracking torque and cracking torque are 7.6% and 12.6% different from those calculated by the finite element method, and the difference of the ultimate torque (considering the tensile strength of C50) is only 2.3%, which verifies the accuracy of the torsional calculation formula derived in this paper.
(3) On the premise that the tensile stress of the bottom slab concrete does not exceed the limit, the initial cracking torque value of the section is controlled by the RC bridge deck, and is not affected by the initial preloading stress and UHPC tensile strength; The initial preloading stress and UHPC tensile strength have a great influence on the cracking torque and ultimate torque of the section. The cracking torque and ultimate torque of the example beam after preloading stress are 115.5% and 57.9% respectively, and the cracking torque and ultimate torque after considering UHPC tensile strength are 261.6% and 94.1% respectively. Properly increasing the initial preloading stress or using hardened UHPC can enhance the cracking torque and ultimate torque of the section.
(4) The initial cracking torque and cracking torque of concrete in tension and compression stress state will be reduced by 8.6% and 13.3% respectively, which should be considered in the calculation.
Abbreviations
UHPC | Ultra High Performance Concrete |
RC | Reinforced Concrete |
Author Contributions
Hanhao Zhang: Conceptualization, Data curation, Software
Xiangdong Sun: Writing - original draft
Dongjin Xu: Writing - review & editing
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
Eugen Brühwiler, Peng Feng, Mohamed Moustafa. Bending resistance mechanism of prestressed ultra-high performance concrete - reinforced concrete beam based on a full-scale experiment [J]. Advances in Structural Engineering, 20240700.
https://doi.org/10.1177/13694332241237578
|
| [2] |
Graybeal B A. Structural behavior of ultra-high performance concrete prestressed I-girders [R]. No. FHWA-HRT-06-115. McLean, VA: Federal Highway Administration, 2006.
https://www.researchgate.net/publication/313505596_Structural_behavior_of_ultra-high_performance_concrete_prestressed_I-Girders
|
| [3] |
JTG 3362-2018, Design Specification for Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. China Communications Press, 2018.
|
| [4] |
EN 1992-2: 2005. Eurocode 2: Design of Concrete Structures-Concrete Bridges Design and Detailing Rules [S]. 2008.
|
| [5] |
NF P 18-710. National addition to Eurocode 2 - Design of concrete structures: specific rules for Ultra-High Performance Fibre-Reinforced Concrete (UHPFRC) [S]. Association Française de Normalisation, 2016.
|
| [6] |
ULTRA HIGH PERFORMANCE FIBRE- REINFORCED (Recommendation, Revised edition) [S]. Association Française de Génie Civil, 2013.
|
| [7] |
Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC) - Construction material, dimensioning and application (Recommendation) [S]. MCS-EPFL Lausanne, Switzerland, 2016.
|
| [8] |
T/CBMF 185-2022, Specifcation for design of ultra-high performance concrete struetures [S]. China Building Materials Industry Press, 2022.
|
| [9] |
T/CECS G: D60-02-2023, Technical Specifications for Highway Ultra-high Performance Concrete (UHPC) Bridges [S]. People's Communications Publishing House Co., Ltd, 2023.
|
| [10] |
JGJ/T 465-2019, Standard for design of steel fiber reinforced concrete structures [S]. China Architecture&Building Press, 2019.
|
| [11] |
ZHOU J, Li C, Experimental investigation on torsional behaviors of ultra-high performance fiber reinforced concrete hollow beams [J]. Cement and Concrete Composites, 2022. CECO: 104504.
https://doi.org/10.1016/j.cemconcomp.2022.104504
|
| [12] |
KWAHK I, JOHC, LEE JW, Torsional behavior design of UHPC box beams based on thin-walled tube theory [J]. Engineering, 2015, 7(3): 101-114.
https://doi.org/10.4236/eng.2015.73009
|
| [13] |
YANG I, JOH C, LEE JW, et al. Torsional behavior of ultra high performance concrete squared beams [J]. Engineering Structures, 2013(56): 372-383.
https://doi.org/10.1016/j.engstruct.2013.05.027
|
| [14] |
Qiu JS. Study on calculation theory and behavior of steel fiber reinforced concrete Multi-ribbed composite slab [D]. Xi'an University of Architecture and Technology, 2011.
|
| [15] |
Ke L, Yu S, Li CX, etc. Torsional Performance and Bearing Capacity Calculation of Reinforced UHPC Rectangular Beams Subjected to Combined Bending-shear-torsion [J]. China Journal of Highway and Transport, 2023, 36(09): 157-171.
https://doi.org/10.19721/j.cnki.1001-7372.2023.09.013
|
| [16] |
Wang JQ, Zhou C, Jia WB, etc. Investigation on the Effect of Steel Fiber Property on the Torsional Performance of Ultra high Performance Concrete Rectangular Beams without Steel Reinforcement [J]. China Journal of Highway and Transport, 2022, 35(12): 115-129.
https://doi.org/10.19721/j.cnki.1001-7372.2022.12.010
|
| [17] |
Zhou C, Wang JQ, Chen JT, etc. Experimental Investigation of a Novel Torsional Strengthening Strategy for RC Beams Based on UHPC [J]. China Journal of Highway and Transport, 2023, 36(09): 119-133.
https://doi.org/10.19721/j.cnki.1001-7372.2023.09.010
|
| [18] |
Li CX, Zhou JL, Ke L, etc. Experimental Investigation and Calculation of the Torsional Capacity of Reinforced UHPC Rectangle Beams [J]. China Journal of Highway and Transport, 2021, 34(08): 118-131.
https://doi.org/10.19721/j.cnki.1001-7372.2021.08.010
|
| [19] |
Li CX, Yu S, Zhou LD, etc. Torsional performance of UHPC beams with flanges and unified formula for characteristic torques [J]. Journal of Civil Engineering, 2023, 56(12): 82-97.
https://doi.org/10.15951/j.tmgcxb.22080863
|
| [20] |
GB 50010-2010, Code for design of concrete structures [S]. China Communications Press, 2015.
|
| [21] |
Wu HL, Sun XD, Ji ZM, etc. Flexural Test on Full-Scale Prestressed UHPC-RC Composite Girder Specimen Without Web Reinforcement and Ultimate Bending Moment Calculation [J]. Bridge Construction, 2024, 54(4).
https://doi.org/10.20051/j.issn.1003-4722.2024.04.008
|
Cite This Article
-
APA Style
Hanhao, Z., Xiangdong, S., Dongjin, X. (2025). Research on Calculation Method of Characteristic Torque of Prestressed UHPC-RC I-Shaped Composite Beam. American Journal of Civil Engineering, 13(4), 222-234. https://doi.org/10.11648/j.ajce.20251304.14
 Copy
|
Copy
|
 Download
Download
ACS Style
Hanhao, Z.; Xiangdong, S.; Dongjin, X. Research on Calculation Method of Characteristic Torque of Prestressed UHPC-RC I-Shaped Composite Beam. Am. J. Civ. Eng. 2025, 13(4), 222-234. doi: 10.11648/j.ajce.20251304.14
 Copy
|
Copy
|
 Download
Download
AMA Style
Hanhao Z, Xiangdong S, Dongjin X. Research on Calculation Method of Characteristic Torque of Prestressed UHPC-RC I-Shaped Composite Beam. Am J Civ Eng. 2025;13(4):222-234. doi: 10.11648/j.ajce.20251304.14
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.ajce.20251304.14,
author = {Zhang Hanhao and Sun Xiangdong and Xu Dongjin},
title = {Research on Calculation Method of Characteristic Torque of Prestressed UHPC-RC I-Shaped Composite Beam
},
journal = {American Journal of Civil Engineering},
volume = {13},
number = {4},
pages = {222-234},
doi = {10.11648/j.ajce.20251304.14},
url = {https://doi.org/10.11648/j.ajce.20251304.14},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajce.20251304.14},
abstract = {The prestressed UHPC-RC I-shaped composite beam is a common new type of beam structure at present, and there is relatively little research on the torsional calculation method for this type of structure. This article first defines the mechanical concept of characteristic torque based on the structural characteristics and different stage stress states of prestressed UHPC-RC I-shaped composite beams. Considering the initial pre stress, UHPC tensile strength, and concrete tensile and compressive stress states, theoretical formulas for initial cracking torque, cracking torque, and ultimate torque are derived based on elastic theory, plastic theory, and variable angle spatial truss theory, respectively; Subsequently, taking a 25m prestressed UHPC-RC I-shaped composite beam as an example, the accuracy of the theoretical formula in this paper was verified through finite element calculation results, where the theoretical value of the ultimate torque differed only 2.3% from the finite element calculation value. Finally, a parametric analysis of the characteristic torque of the beam was conducted, and the results of this study showed that the initial cracking torque value of the section was not affected by the initial pre stress and UHPC tensile strength, provided that the main tensile stress of the bottom concrete did not exceed the limit; Increasing the initial prestressing stress of the section or enhancing the tensile strength of UHPC can enhance the cracking torque and ultimate torque of the section. Considering the initial prestressing stress and UHPC tensile strength, the ultimate torque of the section can be increased by 57.9% and 94.1%, respectively. If the influence of the tensile and compressive stress states of concrete is neglected in the calculation, the values of the initial cracking torque and cracking torque of the section will be overestimated by 8.6% and 13.3%, respectively.},
year = {2025}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Research on Calculation Method of Characteristic Torque of Prestressed UHPC-RC I-Shaped Composite Beam
AU - Zhang Hanhao
AU - Sun Xiangdong
AU - Xu Dongjin
Y1 - 2025/08/05
PY - 2025
N1 - https://doi.org/10.11648/j.ajce.20251304.14
DO - 10.11648/j.ajce.20251304.14
T2 - American Journal of Civil Engineering
JF - American Journal of Civil Engineering
JO - American Journal of Civil Engineering
SP - 222
EP - 234
PB - Science Publishing Group
SN - 2330-8737
UR - https://doi.org/10.11648/j.ajce.20251304.14
AB - The prestressed UHPC-RC I-shaped composite beam is a common new type of beam structure at present, and there is relatively little research on the torsional calculation method for this type of structure. This article first defines the mechanical concept of characteristic torque based on the structural characteristics and different stage stress states of prestressed UHPC-RC I-shaped composite beams. Considering the initial pre stress, UHPC tensile strength, and concrete tensile and compressive stress states, theoretical formulas for initial cracking torque, cracking torque, and ultimate torque are derived based on elastic theory, plastic theory, and variable angle spatial truss theory, respectively; Subsequently, taking a 25m prestressed UHPC-RC I-shaped composite beam as an example, the accuracy of the theoretical formula in this paper was verified through finite element calculation results, where the theoretical value of the ultimate torque differed only 2.3% from the finite element calculation value. Finally, a parametric analysis of the characteristic torque of the beam was conducted, and the results of this study showed that the initial cracking torque value of the section was not affected by the initial pre stress and UHPC tensile strength, provided that the main tensile stress of the bottom concrete did not exceed the limit; Increasing the initial prestressing stress of the section or enhancing the tensile strength of UHPC can enhance the cracking torque and ultimate torque of the section. Considering the initial prestressing stress and UHPC tensile strength, the ultimate torque of the section can be increased by 57.9% and 94.1%, respectively. If the influence of the tensile and compressive stress states of concrete is neglected in the calculation, the values of the initial cracking torque and cracking torque of the section will be overestimated by 8.6% and 13.3%, respectively.
VL - 13
IS - 4
ER -
 Copy
|
Copy
|
 Download
Download
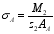 (1)
(1) 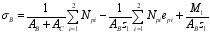 (2)
(2) 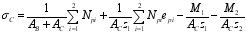 (3)
(3) 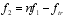 (4)
(4) 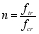 (5)
(5) 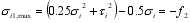 (6)
(6) 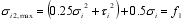 (7)
(7) 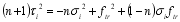 (8)
(8) 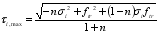 (9)
(9) 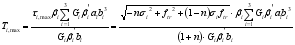 (10)
(10) 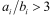 ,
, 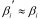 , there are:
, there are: 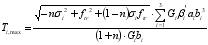 (11)
(11) 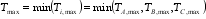 (12)
(12) 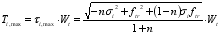 (13)
(13) 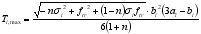 (14)
(14) 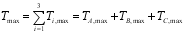 (15)
(15) 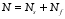 (16)
(16) 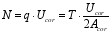 (17)
(17) 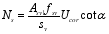 (18)
(18) 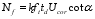 (19)
(19) 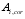 is the core area of section I in the blocking area,
is the core area of section I in the blocking area, 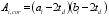 ;
; 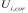 is the perimeter of the core area of section i in the blocking area,
is the perimeter of the core area of section i in the blocking area, 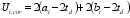 ; k is the fiber orientation coefficient; TD is the wall thickness of the equivalent thin-wall section,
; k is the fiber orientation coefficient; TD is the wall thickness of the equivalent thin-wall section, 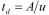 , A is the total area surrounded by the outer periphery of the solid section; u is the outer perimeter of the solid section. The equivalent wall thickness td shall not be less than 2 times of the distance between the outer edge of the section and the center of the longitudinal reinforcement. For hollow sections, the actual wall thickness is the upper limit
, A is the total area surrounded by the outer periphery of the solid section; u is the outer perimeter of the solid section. The equivalent wall thickness td shall not be less than 2 times of the distance between the outer edge of the section and the center of the longitudinal reinforcement. For hollow sections, the actual wall thickness is the upper limit 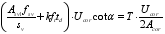 (20)
(20) 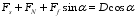 (21)
(21) 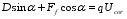 (22)
(22) 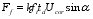 (23)
(23) 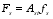 (24)
(24) 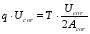 (25)
(25) 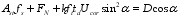 (26)
(26) 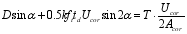 (27)
(27) 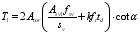 (28)
(28) 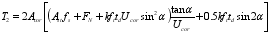 (29)
(29) 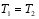 :
: 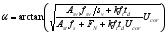 (30)
(30) 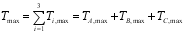 (31)
(31)